整理自此篇.

问题描述：给定一组物品(从1到n)，每种物品都有自己的重量(wi)和价格(vi)，在限定的总重量(W)内，我们如何选择，才能使得物品的总价格最高。

暴力解法：

每个物品要么放进背包，要么不放，都只有两种选择。

如果放进背包，则可放进背包的限定重量变为 W - wi, 已获得价值加vi, 继续检查剩余的物品(n-1)；

如果不放进背包，总价值和可放进背包的限定重量都没有发生改变，继续检查剩余的物品。

它看起来就像下图这样：

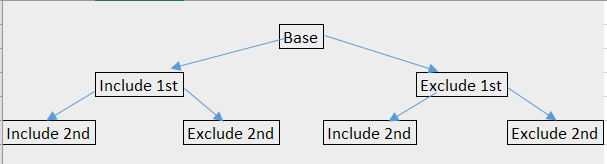
每一层 d 都有 2d个节点，因此n个物品它的复杂度是 2n。

另外一个理解，n个物品，每个物品要么放，要么不放，那么这些物品的可能组合则是2x2x2x…x2,即2n。

动态规划解法：

我们举一个实际的例子，若有3个物品，它们的重量是 weights = { 1, 2, 3 }，价格分别是 values = { 6, 10, 12 }, 我们有一个最多能装5的背包。

现在，我们用一个表格来进行求解：

表格的列是可放进背包的限定重量，从 0 到 5.

表格的每一行，对应每一个物品，我们在前面分别标记了这个物品的重量和价格。

第0行表示0重量(没有物品)的情况，没有物品，所以所有限定重量下的值都是0。

第1行，物品重量是1，限定重量为1到5都能放进去，所以它们的值都是该物品的价格6。

第2行，物品重量是2，当限定重量为2时有两种选择，放或者不放。如果不放，则值仍然保持为上一行中的6。如果放，那么值应该为 

1
当前物品的价格 + d(1, 当前的限定重量 - 准备放进去的物品重量) = 10 + d(1, 2-2) = 10 + 0 = 10

放进去的总价值更大，所以d(2, 2) = 10. 我们使用的公式是

1
d(i, w) = max( d(i - 1, w), d(i - 1, w - weight[i]) + value[i])

例如第3行和限定重量为4的单元格，它的值则是

1
d(3, 4) = max( d(2, 4), d(2, 4-3) + 12 ) = max( d(2, 4), d(2, 1) + 12 ) = 18

以此类推，我们可以得到最大价值是22

不难看出，我们需要计算的次数是N * W. 因此时间复杂度是O(NW)

供参考的C++实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
int knapsack_0_1(int weights[], int values[], int n, int maxWeight)
{
    int **d = new int*[n + 1];
    for (int i = 0; i < n + 1; ++i) {
        d[i] = new int[ maxWeight + 1 ];
    }
    for (int w = 0; w <= maxWeight; w++) {
        d[0][w] = 0;
    }
    for (int i = 0; i < n; i++) {
        for (int w = 0; w <= maxWeight; w++) {
            if (weights[i] <= w) {
                d[i + 1][w] = std::max(d[i][w], d[i][w - weights[i]] + values[i]);
            } else {
                d[i + 1][w] = d[i][w];
            }
        }
    }
    int result = d[n][maxWeight];
    for(int i = 0; i < n; ++i) {
        delete [] d[i];
    }
    delete [] d;
    return result;
}

此算法的核心是避免了重复计算，从而使时间复杂度从O(2n) 降低到了 O(WN)。

Reference